A mathematical object for retrieving the structure of stimuli in EEG data

May 28, 2019

A recent NeuroMat paper has addressed the conjecture that the brain identifies structures from sequences of stimuli. It means that in order to make predictions the brain analyzes structured  sequences of stimuli and retrieves from them statistical regularities. This classical conjecture is often called "Statistician Brain Conjecture" and is associated to studies on how one learns. The NeuroMat research team has introduced a new class of stochastic processes --sequences of random objects driven by chains with memory of variable length-- to address this conjecture.

The paper is "Retrieving a Context Tree from EEG Data" and was published in Mathematics in May. Authors are NeuroMat members Aline Duarte, Ricardo Fraiman, Antonio Galves, Guilherme Ost and Claudia D. Vargas.

An experiment was designed to test the Statistician Brain conjecture. According to the paper, subjects were exposed to a sequence of rhythmic stimuli while electroencephalographic data were recorded. The sequence was formed by strong and weak beats, as well as silences, respectively identified as 2, 1 and 0. It was initially produced as following: "211211211211..." and with some probability a weak beat was replaced by a silence. The hypothesis here was that the way the brain codifies the experiment is a description of the source, so that one could find in the EEG record an encoded signature of the structure of the stimuli.

To model the relationship between the random chain of auditory stimuli and the corresponding EEG data, the authors have introduced a new class of stochastic processes. A process in this class has two components. The first one is a stochastic chain taking values in the set of auditory units. The second one is a sequence of functions corresponding to the sequence of EEG chunks recorded during the exposure of the sequence of rhythmic stimuli.

The structure of the sequence of stimuli was modeled as a stochastic chain with memory of variable length. This mathematical object is used to characterize the dependence from the past in the sequence of rhythmic stimuli. The assumption here is that the dependence from past stimuli has not a fixed length, so that to predict a coming stimulus one might need varying information on the past. Within this framework, a context is defined as the smallest final string of past symbols containing all the information required to predict the next symbol, so that the experimental sequence in the paper can be described as a context tree in which all information required to predicted the next unit of the sequence of stimuli is described, as in the following figure.

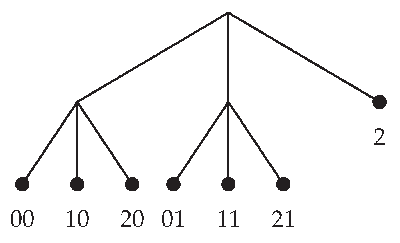
The relationship between the chain of rhythmic stimuli and the chunks of EEG was modeled as following: "at each time step a new EEG chunk is chosen according to a probability measure (defined on suitable class of functions) which depends only on the context assigned to the sequence of auditory units generated up to that time. In particular, this implies that to describe the new class of stochastic chains introduced in this paper, we also need to consider a family of probability measures on the set of functions corresponding to the EEG chunks, indexed by the contexts of the context tree characterizing the chain of auditory stimuli." The paper introduces a statistical procedure to select the sequences of random objects driven by chains with memory of variable length, which is supported theoretically and illustrated with a simulation study.

The paper is part of a sequence of NeuroMat publications on the Statistician Brain Conjecture. Forthcoming pieces will present other experimental protocols and experimental data.

This piece is part of NeuroMat's Newsletter #63. Read more here

Share on Twitter Share on Facebook