A note on supersaturated set systems

Feb 18, 2016

Peter Frankl, Yoshiharu Kohayakawa, Vojtěch Rödl

A well-known theorem of Erdős, Ko and Rado implies that any family ℱ of k-element subsets of an n-element set with more than 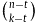members must contain two members F and F' with |F∩F'| < t, as long as n is sufficiently large with respect to k and t. We investigate how many such pairs (F,F') ∈ ℱ×ℱ there must be in any such family ℱ with 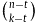and α > 1.

The whole paper is available here.

Share on Twitter Share on Facebook